Michele Coscia

Looking at a population map, one may wonder why sometimes you find metropoles in the middle of nowhere — I’m looking at you, Phoenix. Or why cities are distributed the way they are. When in doubt, you should always refer to your favorite geographer. She would probably be very happy to direct your interest to the Central Place Theory (CPT), developed by Walter Christaller in the 30s. The theory simply states that cities provide services to the surrounding areas. As a consequence, the big cities will provide many services and small cities a few, therefore the small cities will gravitate around larger settlements. This smells like complexity science to me and this post is exactly about connecting CPT with my research on retail customer sophistication and mobility. But first I need to convince you that CPT actually needs this treatment.

CPT explains why sometimes you will need a big settlement in the middle of the desert. That is because, for most of history, civilizations relied on horses instead of the interwebz for communication and, with very long stretches of nothing, that system would fall apart. That is why Phoenix has been an obsolete city since 1994 at the very least, and people should just give it up and move on. You now might be tempted to take a look at the Wikipedia page of the Central Place Theory to get some more details. If you do, you might notice a few “simplifications” used by Christaller when developing the theory. And if you don’t, let me spoil it for you. Lo and behold, to make CPT work we need:

• An infinite flat Earth — easy-peasy-lemon-squeezy compared to what comes next;
• Perfectly homogeneous distribution of people and resources;
• Perfectly equidistant cities in a grid much like the one of Civilization 5;
• The legendary perfect competition and rational market conjured by economists out of thin air;
• Only one mode of transportation;
• A completely homogeneous population, all equal in desires and income.

In short, the original CPT works in a world that is no more real than Mordor.

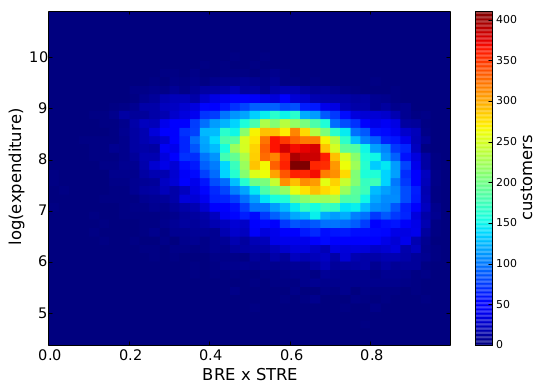
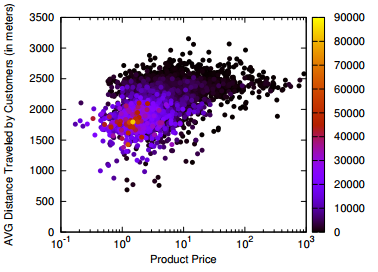
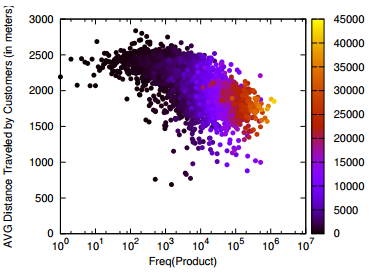
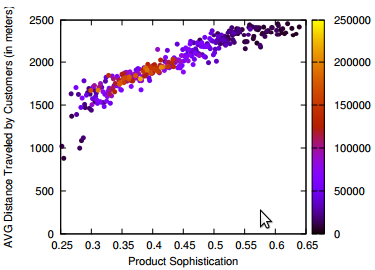
And here where’s sophistication comes into play. I teamed up with Diego Pennacchioli and Fosca Giannotti with the objective of discovering the relationship between CPT and our previous research on sophistication — the result is in the paper Product Assortment and Customer Mobility, just published on EPJ Data Science. In the past, we showed that the more sophisticated the needs of a customer, the further the customer is willing to travel to satisfy those. And our sophistication measure worked better than other product characteristics, such as the price and its average selling volume.

Now, to be honest, geographers did not sleep for 80 years, and they already pointed out the problems of CPT. Some of them developed extensions to get rid of many troubling assumptions, others tested the predictions of these models, others just looked at Phoenix in baffled awe. However, without going too in depth (I’m not exactly qualified to do it) these new contributions are either very theoretical in nature, or they haven’t used larger and more detailed data validation. Also, the way central places are defined is unsatisfactory to me. Central places are either just very populous cities, or cities with a high variety of services. For a person like me trained in complexity science, this is just too simple. I need to bring sophistication into the mix.

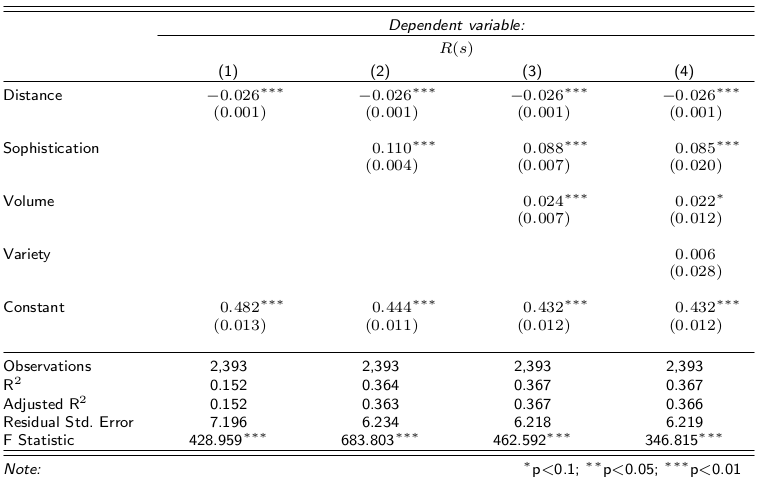
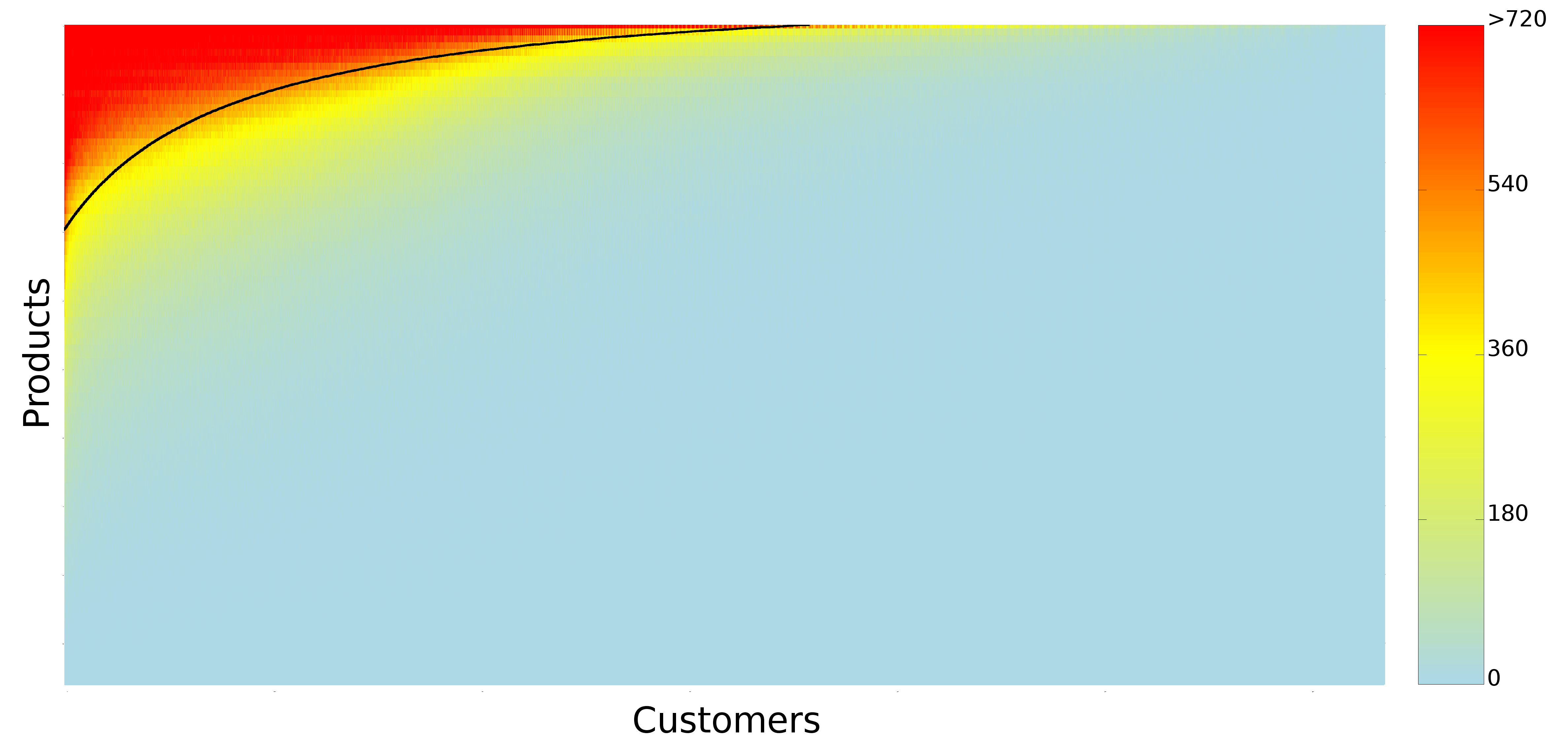
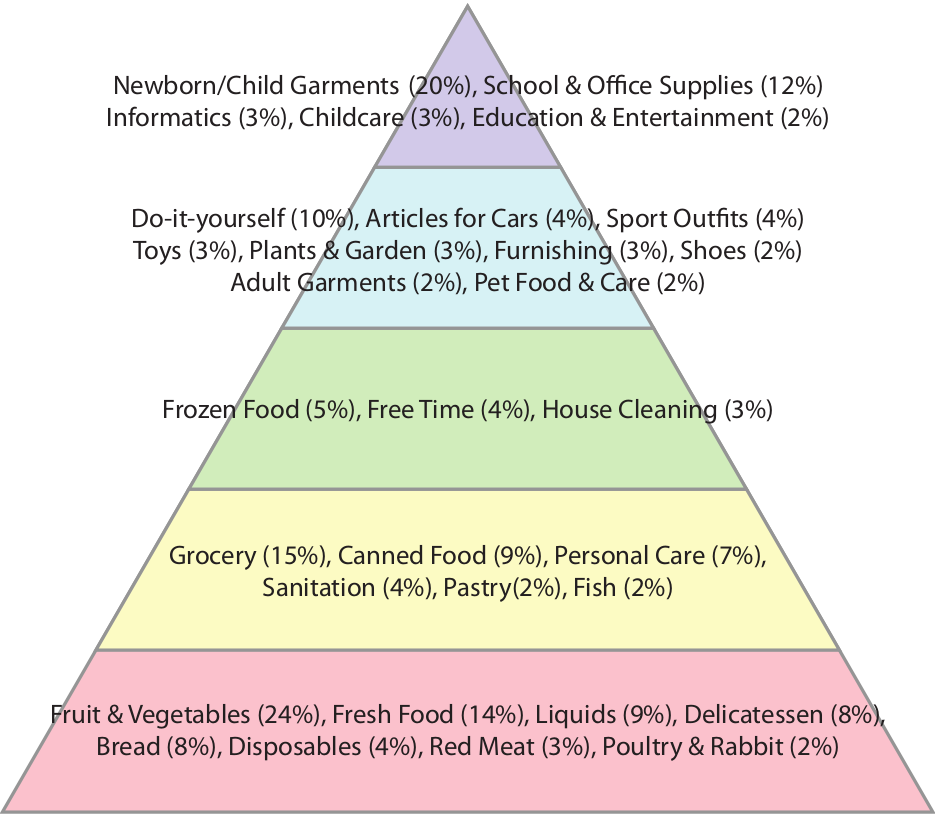
Focusing on my supermarket data, variety is the number of different products provided. Two supermarkets selling three items have the same variety. Sophistication requires the products not only to be different, but also to satisfy different needs. Suppose shop #1 sells water, juice and soda, and shop #2 sells water, bread and T-shirts. Even if the shops have the same variety, one is more sophisticated than the other. And indeed the sophistication of a shop explains better the “retention rate” of a shop, its ability to preserve its customer base even for customers who live far away from the shop. That is what the above table reports: controlling for distance (which causes a 2.6 percentage point loss of customer base per extra minute of travel), each standard deviation increase in sophistication strengthens the retention rate by 11 percentage points. Variety of products does not matter, the volume of the shop (its sheer size) matters just a bit.

In practice, what we found is that CPT holds in our data where big supermarkets play the role of big cities and provide more sophisticated “services”. This is a nice finding for two reasons. First, it confirms the intuition of CPT in a real world scenario, making us a bit wiser about the world in which we live — and maybe avoiding mistakes in the future, such as creating a new Phoenix. This is non-trivial: the space in our data is not infinite, homogeneous, with a perfect market and it has differentiated people. Yet, CPT holds, using our sophistication measure as driving factor. Second, it validates our sophistication measure in a theoretical framework, potentially giving it the power to be used more widely than what we have done so far. However, both contributions are rather theoretical. I’m a man of deeds, so I asked myself: are there immediate applications of this finding?

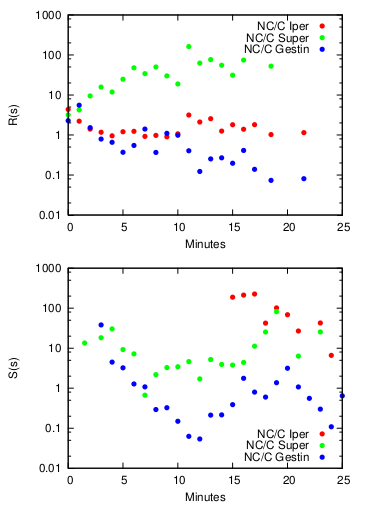
There might be one, with caveats. Remember we are analyzing hundreds of supermarkets in Italy. We know things about these supermarkets. First, we have a shop type, which by accident correlates with sophistication very well. Then, we know if the shop was closed down during the multi-year observation period. We can’t know the reason, thus everything that follows is a speculation to be confirmed, but we can play with this. We can compare the above mentioned retention rate of closing and non-closing shops. We can also define a catch rate. While “retention” meant how many of your closest customers you can keep, catch means how many of the non-closest customers you can get. The above plots show retention and catch ratios. The higher the number the more the ratio is in favor of the non-closing shop.

For the retention rate, the average sophistication shops (green) have by far the largest spread between shops that are still open and the ones which got shut down. It means that these medium shops survive if they can keep their nearby customers. For the catch rate, the very sophisticated shops (red) are always on top, regardless of distance. It means that large shops survive if they really can attract customers, even if they are not the closest shop. The small shops (blue) seem to obey neither logic. The application of this finding is now evident: sophistication can enlighten us as to the destiny of different types of shops. If medium shops fail to retain their nearby customers, they’re likely to shut down. If large shops don’t catch a wider range of customers, they will shut down. This result talks about supermarkets, but there are likely connections with settlements too, replacing products with various services. Once we calculate a service sophistication, we could know which centers are aptly placed and which ones are not and should be closed down. I know one for sure even without running regressions: Phoenix.

Continue Reading

I don’t know about you guys, but when it comes to groceries I show behaviors that are strongly reminiscent of Rain Man. I go to the supermarket the same day of the week (Saturday) at the same time (9 AM), I want to go through the shelves in the very same order (the good ol’ veggie-cookies-pasta-meat-cat food track), I buy mostly the same things every week. Some supermarkets periodically re-order their shelves, for reasons that are unknown to me. That’s enraging, because it breaks my pattern. The mahātmā said it best:

Amen to that. As a consequence, I signed up immediately when my friends Riccardo Guidotti and Diego Pennacchioli told me about a paper they were writing about studying the regularity of customer behavior. Our question was: what is the relationship between the regularity of a customer’s behavior and her profitability for a shop? The results are published in the paper “Behavioral Entropy and Profitability in Retail“, which will be presented in the International Conference on Data Science and Advanced Analytics, in October. To my extreme satisfaction the answer is that the more regular customers are also the most profitable. I hope that this cry for predictability will reach at least the ears of the supermarket managers where I shop. Ok, so: how did we get to this conclusion?

First, we need to measure regularity in a reasonable way. We propose two ways. First, a customer is regular if she buys mostly the same stuff every time she shops, or at least her baskets can be described with few typical “basket templates”. Second, a customer is regular if she shows up always at the same supermarket, at the same time, on the same day of the week. We didn’t have to reinvent the wheel to figure out a way for evaluating regularity in signals: giants of the past solved this problem for us. We decided to use the tools of information theory, in particular the concept of information entropy. Information entropy tells how much information there is in an event. In general, the more uncertain or random the event is, the more information it will contain.

If a person always buys the same thing, no matter how many times she shops, we can fully describe her purchases with a single bit of information: the thing she buys. Thus, there is little information in her observed shopping events, and she has low entropy. This we call Basket Revealed Entropy. Low basket entropy, high regularity. Same reasoning if she always goes to the same shop, and we call this measure Spatio-Temporal Revealed Entropy. Now the question is: what does happen to a customer’s expenditure for different levels of basket and spatio-temporal entropy?

To wrap our heads around these two concepts we started by classifying customers according to their basket and spatio-temporal entropy. We used the k-Means algorithm, which simply tries to find “clumps” in the data. You can think of customers as ants choosing to sit in a point in space. The coordinates of this point are the basket and spatio-temporal entropy. k-Means will find the parts of this space where there are many ants nearby each other. In our case, it found five groups:

1. The average people, with medium basket and spatio-temporal entropy;
2. The crazy people, with unpredictable behavior (high basket and spatio-temporal entropy);
3. The movers, with medium basket entropy, but high spatio-temporal entropy (they shop in unpredictable shops at unpredictable times);
4. The nomads, similar to the movers, with low basket entropy but high spatio-temporal entropy;
5. The regulars, with low basket and spatio-temporal entropy.

Click to enlarge

Once you cubbyholed your customers, you can start doing some simple statistics. For instance: we found out that the class E regulars spend more per capita over the year (4,083 Euros) than the class B crazy ones (2,509 Euros, see the histogram above). The regulars also visit the shop more often: 163 times a year. This is nice, but one wonders: why haven’t the supermarket managers figured it out yet? Well, they may have been, but there is also a catch: incurable creatures of habit like me aren’t a common breed. In fact, if we redo the same histograms looking at the group total yearly values of expenditures and baskets, we see that class E is the least profitable, because fewer people are very regular (only 6.9%):

Click to enlarge

Without dividing customers in discrete classes, we can see what is the direct relationship between behavioral entropy and the yearly expenditure of a customer. This aggregated behavioral entropy measure is simply the multiplication of basket and spatio-temporal entropy. Unsurprisingly, entropy and expenditure are negatively correlated:

Finally, we want to quantify this relationship. We want to have an objective way to tell how much more money the supermarket could make if the customers would be more regular. We didn’t get too fancy here, just a linear model where we try to predict the customers’ expenditures from their basket and spatio-temporal entropy. We don’t care very much about causation here, we just want to make the point that basket and spatio-temporal entropy are interesting measures.

Click to enlarge

The negative sign isn’t a surprise: the more chaotic a customer’s life, the lower her expenditures. What the coefficients tell us is that we expect the least chaotic (0) customer to spend almost four times as much as the most chaotic (1) customer*. You can understand why this was an extremely pleasant finding for me. This week, I’m going to print out the paper and ask to see the supermarket manager. I’ll tell him: “Hey, if you stop moving stuff around and you encourage your customers to be more and more regular, maybe you could increase your revenues”. Only that I won’t do it, because that’d break my Saturday shopping routine. Oh dear.

* The interpretation of coefficients in regressions are a bit tricky, especially when transforming your variables with logs. Here, I just jump straight to the conclusion. See here for the full explanation, if you don’t believe me.

Continue Reading

There are few things that you would consider less interesting than doing groceries at the supermarket. For some it’s a chore, others probably like it. But for sure you don’t see much of a meaning behind it. It’s not that you sense around you a grave atmosphere, the kind of mysterious background radiance you perceive when you feel part of Something Bigger. Just buy the bloody noodles already. Well, to some extent you are wrong.

(Image from “Hungry Planet: What the World Eats“)

Of course the reality is less mystical than what I tried to led you to believe in this opening paragraph. But it turns out that customers of a supermarket chain behave as if they were playing a specific role. These roles are the focus of the paper I recently authored with Diego Pennacchioli, Salvatore Rinzivillo, Dino Pedreschi and Fosca Giannotti. It has been published on the journal EPJ Data Science, and you can read it for free.

So what are these roles? The title of the paper is very telling: the retail market is a complex system. So the first thing to clear out is what the heck a complex system is. This is not so easily explained – otherwise it wouldn’t be complex, duh. The precise physics definition of complex systems might be too sophisticated. For this post, it will be sufficient to use the following one: a complex system is a collection of interacting parts and its behavior cannot be expressed as a sum of the behaviors of its parts. A good example of complexity is Earth’s ecosystem: there are so many interacting animals and phenomena that having a perfect description of it by just listing all interactions is just impossible.

And a supermarket is basically the same. In the paper we propose several proofs of it, but the one that goes best with the chosen example involves the esoteric word “nestedness”. When studying different ecosystems, some smart dudes decided to record their observations in matrix form. For each different island (ecosystem) they recorded if a particular species was present or not. When they looked at the resulting matrix they noticed a particular pattern. The islands with few species had only the species that were found in all islands, and at the same time the most rare species were present exclusively in those islands which were hosting all the observed species. If you reordered the islands by species count and the species by island count, the matrix had a particular triangular shape. They called matrices like that “nested”.

We did the same thing with customers and products. There are customers who buy only a handful of products: milk, water, bread. And those products are the products that everybody buys. Then there are those customers who, over a year, buy basically everything you can see in a supermarket. And they are the only ones buying the least sold products. The customers X products matrix ends up looking exactly like an ecosystem nested matrix (you probably already saw it over a year ago on this blog – in fact, this work builds on the one I wrote about back then, but the matrix picture is much prettier, thanks to Diego Pennacchioli):

Since we have too many products and customers, this is a compressed view and the color tells you how many observations we have per pixel (click for full resolution). One observation is simply a pairing of a customer and a product, indicating that the customer bought that product in significant quantities over a year. Ok, where does this bring us? First, as parts of a complex system, customers are not so easily classifiable. Marketing is all about finding uniformly behaving groups of people. The consequence of being complex parts is that this task is hopeless. You cannot really put people into bins. People are part of a continuous space, as shown in the picture, and every cut-off you propose is necessarily arbitrary.

The solution to this problem is represented by that black line you see on the matrix. That line is trying to divide the matrix in two parts: a part where we mostly have ones, and a part where we mostly have zeroes. The line does not match reality perfectly. It is a hyperbola that we told to fit itself as snugly to the data as possible. Once estimated, the function of the black line enables a neat application: to predict the next product a customer is interested in buying.

Remember that the matrix has its columns and rows sorted. The first customer is the one who bought the most products, the second bought a little less product and so on with increasing ranks. Same thing with products: the highest ranked (1st) is sold to most customers, the lowest ranked is sold to just one customer. This means that if you have the black line formula and the rank of a customer, you can calculate the rank of a corresponding product. Given that the black line divides the ones from the zeros, this product is a zero that can most easily become a one or, in other words, the supermarket’s best bet of what product the customer is most likely to want to buy next. You do not need customer segmentation any more: since the matrix is and will always be nested you just have to fill it following the nested pattern, and the black line is your roadmap.

We can use the ranks of the products for a description of customer’s needs. The highest ranked products are bought by everyone, so they are satisfying basic needs.  We decided to depict this concept borrowing Maslow’s pyramid of needs. The one reported above is interesting (again, click for full resolution), although it applies only to the supermarket area our data is coming from. In any case it is interesting how some things that are on the basis of Maslow’s pyramid are on top of our, for example having a baby. You could argue that many people do not buy those products in a supermarket, but we address these concerns in the paper.

So next time you are pondering whether buying or not buying that box of six donuts remember: you are part of a gigantic system and the little weight you might gain is insignificant compared to the beautiful role you are playing. So go for it, eat the hell out of those bad boys.

Continue Reading

The Holy Grail of every marketing system is to understand how the mind of the customers works. For example answering the question: “From how far can I attract customers?” To do so means to increase profits. You can deploy your communication and products more efficiently and maximize your returns. Clearly, there is no silver bullet for this task. There is no way that one single aspect is so predominant in a person’s mind at the point of empowering a seller to have perfect control over who will buy her product, where and when. If that would be true, there would be no space left for marketing specialists, demand segmentation and so on. Many little tricks can be deployed in the market.

I am by no means an expert on the field, so my way to frame this problem may sound trivial. In any case, I can list three obvious parameters that affect a customer’s decision in buying or not buying a product. The first is price. Few people want to throw their money senselessly, most of them want to literally maximize the bang for their buck (okay, maybe not that literally). The second is the quantities needed: if I need to buy product X everyday in large bulks and product Y once in a blue moon, then it’s only fair to assume that I’ll consider different parameters to evaluate X and Y.

The third is the level of sophistication of a given product. There are things that fewer and fewer people need: birdseed, piña colada flavored lip balm. Narrower customer base means less widespread offer, thus the need of travel more to specialized shops. Intuitively, sophistication is more powerful than price and quantity: a Lamborghini is still a car – also quite useless when doing groceries – like a Panda, but it satisfies very different and much more sophisticated needs. Sophistication is powerful because you can play with it, increasing the perceived sophistication of a product, thus your market: like Jonah Berger‘s  “thee types of ice” bar, that looked more fancy just by inventing a way to make ice sound more sophisticated than it is.

So let’s play and try to use these concepts operatively. Say we want to predict the distance a customer is willing to travel to buy a product. Then, we try to predict such a distance using different variables. The one leading to better predictions of these distances wins as the best variable describing what motivates a customer to travel. We decided to test the three variables I presented before: price, quantity and sophistication. In this theory, higher prices mean longer distances to travel, as if I have to buy an expensive TV I’ll probably go around and check where is the best quality-price ratio. Higher quantities mean shorter distances, as if I have to buy bread everyday I don’t care where the best bakery of the city is if that means traveling ten kilometers everyday. Finally, higher sophistication means longer distances: if I have sophisticated needs I need to travel a lot to satisfy them.

Price and quantity are easy to deal with: they are just numbers. So we can put them on the X axis of a plot and put the distance traveled on the Y axis. And that’s what we did, for price:

and for quantity:

Here, each dot is a customer buying a product. If the dots had the same distance and the same price/quantity then we merged them together (brighter color = more dots here). We see that our theory, while not perfect, is correct: higher prices means longer distances traveled, higher quantities means shorter distances. Time to test for the level of sophistication! But now we hit a brick wall. How on earth am I suppose to measure the level of sophistication of a person and of a product? Should I split the brain of that person in half? How can I do this for thousands or millions of customers? We need to invent a brain splitting machine.

That’s more or less what we did. In a joint work with Diego Pennacchioli, Salvo Rinzivillo, Fosca Giannotti and Dino Pedreschi, that will appear in the BigData 2013 conference (you can download the paper, if you are interested), we proposed such a brain slice device. Of course I am somewhat scared by all the blood that would result in literally cutting open thousands of skulls, so we implemented a data mining machine that just quantifies with a number the level of sophistication of a customer’s needs and the level of sophistication that a product can satisfy, solving the issue at hand with no bloodshed.

The fundamental question is: is the level of sophistication a number? Intuition would tell us “no”: it’s a complex multidimensional space and my needs are unique like a snowflake. Kind of. But with a satisfying level of approximation, surprisingly, we can describe sophistication with a number. How is that possible? A couple of facts we discovered: customers buying the least sold products also buy everything else (the “simpler” stuff), and products bought just by few customers are bought only by those who also buy everything else. In other words, if you draw a matrix connecting the customers with the products they buy, this matrix is nested, meaning that all purchases are in the top left corner:

A-ha! Then it’s fair to make this assumption: customers are adding an extra product bought only if they already buy (almost) everything else “before” it. This implies two things: first, is that they add the extra product if all their previous products already satisfied their more basic needs (then, they are more sophisticated); second, is that they are moving on a monodimensional space, adding stuff incrementally. Then, they can be quantified by a number! I won’t go in the boring details about how to calculate this number. Suffice to say that they are very similar to how you calculate a country’s complexity, about which I wrote months ago; and that this number is not the total amount of money they spend, nor the quantity of products they buy.

So, how does this number relate to the distance traveled by customers?

The words you are looking for is “astonishingly well”.

So our quantification of the sophistication level has a number of practical applications. In the paper we explore the task of predicting in which shop a customers will go to buy a given product. We are not claiming that this is the only important factor. But it gives a nice boost. Over a base accuracy of around 53%, using the price or the quantity gives you a +6-7% accuracy. Adding the sophistication level gives an additional +6-8% accuracy (plots would suggest more, but they are about continuous numbers, while in reality shop position is fixed and therefore a mistake of a few hundreds meters is less important). Not bad!

Continue Reading