Michele Coscia

Last year I was talking with a non-Italian, trying to convey to them how nearly the entirety of contemporary Italian music rests on the shoulders of Gianni Maroccolo — and the parts that don’t, should. In an attempt to find a way out of that conversation, they casually asked “wouldn’t it be cool to map out who collaborated with whom, to see whether it is true that Maroccolo is the Italian music Messiah?” That was very successful of them, because they triggered my network scientist brain: I stopped talking, and started thinking about a paper on mapping Italian music as a network and analyzing it.

One year later, the paper is published: “Node attribute analysis for cultural data analytics: a case study on Italian XX–XXI century music,” which appeared earlier this month on the journal Applied Network Science.

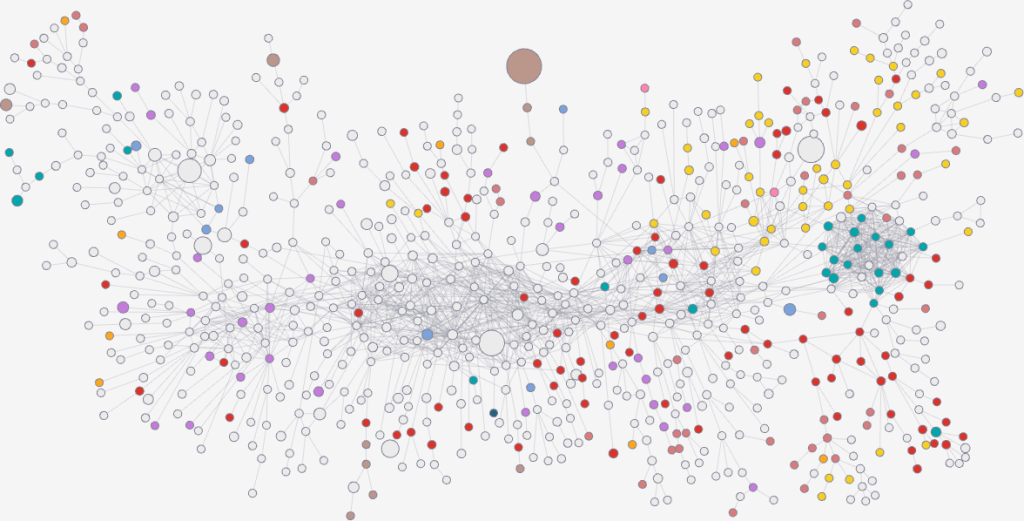
I spent the best part of last year crawling the Wikipedia and Discogs pages of almost 2,500 Italian bands. I recorded, for each album they released, the lineup of the song players and producers. The result was a bipartite network, connecting artists to the bands they contributed to. I tried to have a broad temporal span, starting from the 1902 of Enrico Caruso — who can be considered the first Italian musician of note (hehe) releasing actual records — until a few of the 2024 records that were coming out as I was building the network — so the last couple of years’ coverage is spotty at best.

Then I could make two projections of this network. In the first, I connected bands together if they shared a statistically significant number of players over the years. I used my noise corrected backboning here, to account for potential missing data and spurious links.

This is a fascinating structure. It is dominated by temporal proximity, as one would expect — it’s difficult to share players if the bands existed a century apart. This makes a neat left-to-right gradient timeline on the network, which can be exploited to find eras in Italian music production by using my node attribute distance measure:

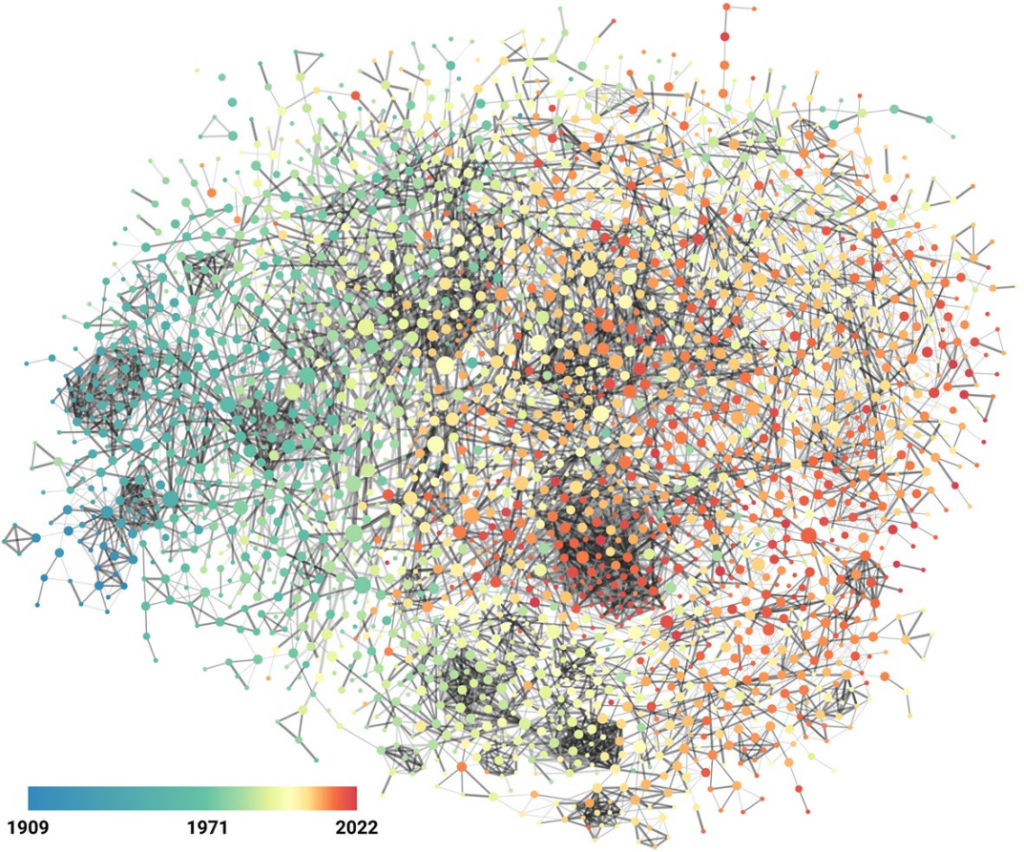
You can check the paper for the eras I found. By using network variance you can also figure out which years were the most dynamic, in terms of how structurally different the bands releasing music in those years were:

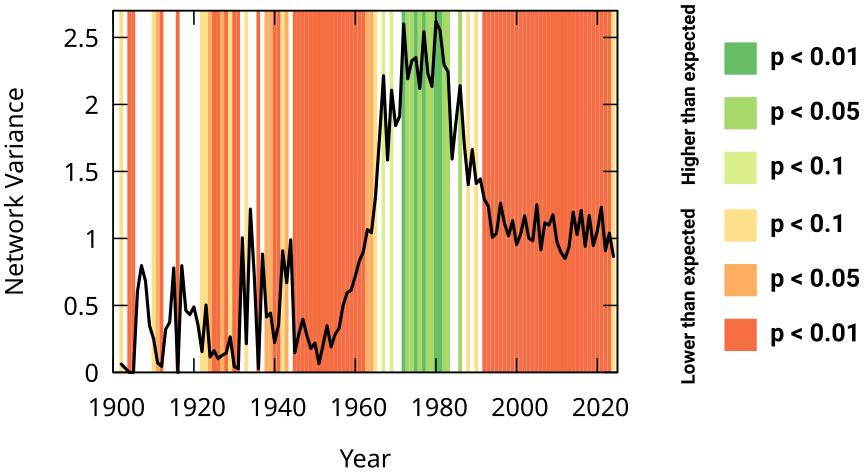
Here we discover that the most dynamic years in Italian music history were from the last half of the 1960s until the first half of the 1980s.

There is another force shaping this network: genre. The big three — pop, rock, electronic — create clear genre areas, with the smaller hip hop living at the intersection of them:

Just like with time, you can use the genre node attributes distances to find a genre clusters, through the lens of how they’re used in Italian music.

What about Maroccolo? To investigate his position, we need to look at the second projection of the artist-band bipartite network: the one where we connect artists because they play in the same bands. Unfortunately, it turns out that Maroccolo is not in the top ten most central nodes in this network. I checked the degree, closeness, and betweenness centralities. The only artist who was present in all three top ten rankings was Paolo Fresu, to whom I will hand over the crown of King of Italian Music.

Continue Reading

I’ve been a longtime fan of measuring distances between node attributes on networks: I’ve reviewed the methods to do it and even proposed new ones. One of the things bothering me was that no one had so far tried to extend these methods to multilayer networks — networks with more than one type of relationships. Well, it bothers me no more, because I just made the extension myself! It is the basis of my new paper: “Generalized Euclidean Measure to Estimate Distances on Multilayer Networks,” which has been published on the TKDD journal this month.

You might be wondering: what does it mean to “measure the distance between node attributes on networks”? Why is it useful? Let’s make a use case. The Product Space is a super handy network connecting products on the global trade network based on their similarity. You can have attributes saying how much of a product a country exported in a given year — in the image above you see what Egypt exported in 2018. This is super interesting, because the ability of a country to spread over all the products in the Product Space is a good predictor of their future growth. The question is: how can we tell how much the country moved in the last ten years? Can we say that country A moved more or less than country B? Yes, we can! Exactly by measuring the distance between the node attributes on the network!

The Product Space is but an example of many. One can estimate distances between node attributes when they tell you something about:

• When and how much people were affected by a disease in a social network;
• Which customers purchased how many products in a co-purchase network (à la Amazon);
• Which country an airport belongs to in a flight network;
• etc…

Let’s focus on that last example. In this scenario, each airport has an attribute per country: the attribute is equal to 1 if the airport is located in that country, and 0 otherwise. The network connects airports if there is at least a flight planned between them. In this way, you could calculate the network distance between two countries. But wait: it’s not a given that you can fly seamlessly between two countries even if they are connected by flights across airports. You could get from airport A to airport B using flight company X, but it’s not a given than X provides also a flight to airport C, which might be your desired final destination. You might need to switch to airline Y — the image above shows the routes of four different companies: they can be quite different! Switching between airlines might be far from trivial — as every annoyed traveler will confirm to you –, and it is essentially invisible to the measure.

It becomes visible if, instead of using the simple network I just described, you use a multilayer network. In a multilayer network, you can say that each airline is a layer of the network. The layer only contains the flight routes provided by that company. In this scenario, to go from airport A to airport C, you pay the additional cost of switching between layers X and Y. This cost can be embedded in my Generalized Euclidean measure, and I show how in the paper — I’ll spare you the linear algebra lingo.

One thing I’ll say — though — is that there are easy ways to embed such layer-switching costs in other measures, such as the Earth’s Mover Distance. However, these measures all consider edge weights as costs — e.g., how long does it take to fly from A to B. My measure, instead, sees edge weights as capacities — e.g. how many flights the airline has between A and B. This is not splitting hairs, it has practical repercussions: edge weights as costs are ambiguous in linear algebra, because they can be confused with the zeros in the adjacency matrices. The zeros encode absent edges, which are effectively infinite costs. Thus there is an ambiguity* in measures using this approach: as edges get cheaper and cheaper they look more and more like infinitely costly. No such ambiguity exists in my approach. The image above shows you how to translate between weights-as-costs and weights-as-capacities, and you can see how you can get in trouble in one direction but not in the other.

In the paper, I show one useful case study for this multilayer node distance measure. For instance, I am able to quantify how important the national flagship airline company is for the connectivity of its country. It’s usually extremely important for small countries like Belgium, Czechia, or Ireland, and less crucial for large ones like France, the UK, or Italy.

The code I developed to estimate node attribute distances on multilayer networks is freely available as a Python library — along with data and code necessary to replicate the results. So you have no more excuses now: go and calculate distances on your super complex super interesting networks!

---

* This is not completely unsolvable. I show in the paper how one could get around this. But I’d argue it’s still better not to have this problem at all 🙂

Continue Reading