Michele Coscia

There was a nice paper published a while ago by the excellent Taha Yasseri showing that soccer is becoming more predictable over time: from the early 90s to now, models trying to guess who would win a game had grown in accuracy. I got curious and asked myself: does this hold only for soccer, or is it a general phenomenon across different team sports? The result of this question was the paper: “Which sport is becoming more predictable? A cross-discipline analysis of predictability in team sports,” which just appeared on EPJ Data Science.

My idea was that, as there is more and more money and professionalism in sport, those who are richer will become stronger over time, and dominate for a season, which will make them more rich, and therefore more dominant, and more rich, until you get Juventus, which came in first or second in almost 50% of the 119 soccer league seasons played in Italy.

My first step was to get data about 300,000 matches played across 49 leagues in nine disciplines (baseball, basket, cricket, football, handball, hockey, rugby, soccer, and volleyball). My second step was to blatantly steal the entire methodology from Taha’s paper because, hey, why innovate when you can just copy the best? (Besides, this way I could reproduce and confirm their finding, at least that’s the story I tell myself to fall asleep at night)

The first answer I got was that Taha was right, but mostly only about soccer. Along with volleyball (and maybe baseball) it is one of the few disciplines that is getting more predictable over time. The rest of the disciplines are a mixed bag of non-significant results and actual decreases in predictability.

One factor that could influence these results is home advantage. Normally, the team playing home has slighter higher odds of winning. And, sometimes, not so slight. In the elite rugby tournament in France, home advantage is something like 80%. To give an idea, 2014 French champions Toulon only won 4 out of their 13 away games, and two of them were against the bottom two teams of the league that got relegated that season.

Well, this is something that actually changed almost universally across disciplines: home advantage has been shrinking across the board — from an average of 64% probability of home win in 2011 to 55% post-pandemic. The home advantage did shrink during Covid, but this trend started almost a decade before the pandemic. The little bugger did nothing to help — having matches played behind closed doors altered the dynamics of the games –, but it only sped up the trend, it didn’t create it.

What about my original hypothesis? Is it true that the rich-get-richer effect is behind predictability? This can be tested, because most American sports are managed under a socialist regime: players have unions, the worst performing teams in one season can pick the best rookies for the next, etc. In Europe, players don’t have unions and if you have enough money you can buy whomever you want.

When I split leagues by the management system they follow, I can clearly see that indeed those under the European capitalistic system tend to be more predictable. So next time you’re talking with somebody preaching laissez-faire anarcho-capitalism tell them that, at least, under socialism you don’t get bored at the stadium by knowing in advance who’ll win.

Continue Reading

If there is a thing that I love more than looking at silly pictures on the Interwebz for work is to watch rugby for work. I love rugby: in my opinion it is the most beautiful team sport out there. It tingles my network senses: 15 men on the field have to coordinate like a single organism to achieve their goal — crossing the goal line with the ball by passing it backwards instead of forward. When Optasports made available some data collected during 18 rugby matches I felt I could not miss the opportunity for some hardcore network nerding on them. The way teams weave their collaboration networks during a match must have some relationship with their performance, and I was going to find out what this relationship might be.

For my quest I teamed up with Luca Pappalardo and Paolo Cintia, two friends of mine who are making an impact on network and big data sports analytics, both in soccer and in cycling. The result was “The Haka Network: Evaluating Rugby Team Performance with Dynamic Graph Analysis“, a paper recently presented at the DyNo workshop in San Francisco. Our questions were:

1. Is there a relationship between the topology of the network of passes and the success of the team?
2. Is there a relationship between disruptions made by tackles and territorial gains?
3. If we want to predict a team’s success, is it better to build networks of passes and disruptions for each action separately or for the entire match?
4. Can we use these relationships to “predict” the outcome of the match?

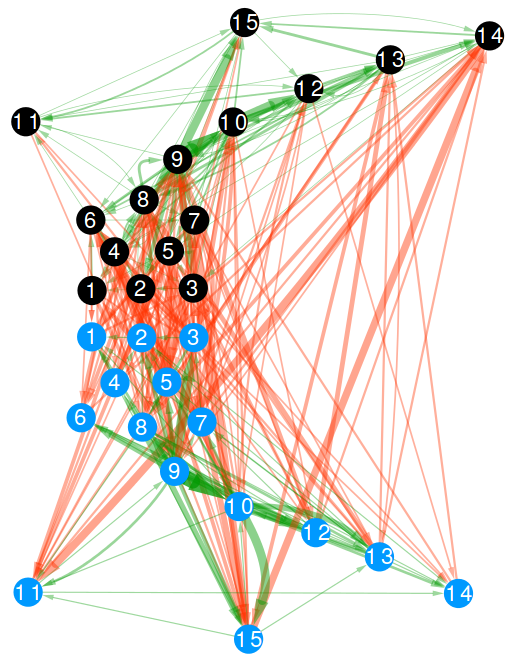
A passage network is simply a network whose nodes are the players of a team and the directed connections go from the player originating a pass to the player receiving the ball. We consider only completed passages: the ones that did not result in an error or lost possession. In the above picture, those are the green edges and they are always established between players belonging to the same team. In rugby, players are allowed to tackle the current ball carrier of the opponent team. When that happens, we create another directed edge, this time in what we call “disruption network”. The aim of a tackle is to prevent the opponent team from gaining meters. These are the red edges in the above picture and can only be established between players belonging to opposite teams. The picture you see is the collection of all passes and tackles which happened in the Italy vs New Zealand match in 2012. It is a multilayer network as it contains edges of two different types: passes and tackles.

Once we have pass and disruption networks we can calculate a collection of network measures. I’ll give a brief idea here, but if you are looking for more formal definitions you’ll have to search for them in the paper:

• Connectivity: how many pass connections you have to remove to isolate players;
• Assortativity: the tendency of players to pass the ball to players with a similar number of connections — in high assortativity central players pass to other central players and marginal players to other marginal players;
• Components: how many “sinks” there are, in that the ball never goes back to the bulk of the team when it is passed to a player in a sink;
• Clustering: how many triangles there are, meaning that the team can be decomposed in many different smaller sub-teams of three players.

These are the features we calculated for the pass networks. The disruption case is slightly different. We calculated the same features for the team when removing the tackled player, weighted on the relative number of tackles. If 50% of the tackles hit player number 11, then 50% of the disrupted connectivity is the connectivity value of the pass network when removing player 11. The reason is that the tackled player is temporarily removed from the game, so we need to know how the team performs without him, weighted on the number of times this occurrence happens.

So, it is time to give some answers. Shall we?

1. Is there a relationship between the topology of the network of passes and the success of the team?

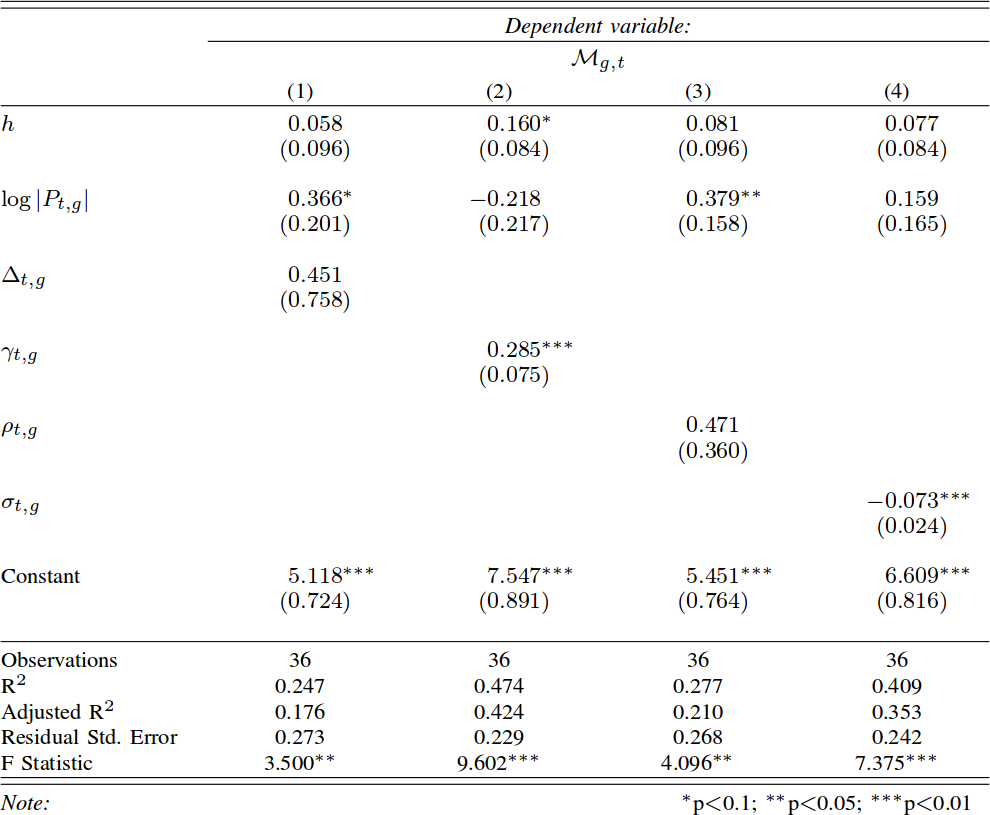
Yes, there is. We calculate “success” as the number of meters gained, ball in hand, by the team. The objective of rugby is to cross the goal line carrying the ball, so meters made is a pretty good indicator. We control for two things. First, the total number of passes: it simply means the team was able to hold onto the ball longer, so it is trivially expected to result in more meters. Second, the home advantage, which is a huge factor in rugby: Italy won only 12 out of 85 matches in the European “Six Nations” tournament, and 11 of them were in Italy. After these controls, we find that two features have good correlations with meters made: connectivity and components. The more edges are needed to isolate a player, the more meters a team is expected to make (p < .01, R2 = 47%). More sinks in a team is associated with lower gains in meters.

2. Is there a relationship between disruptions made by tackles and territorial gains?

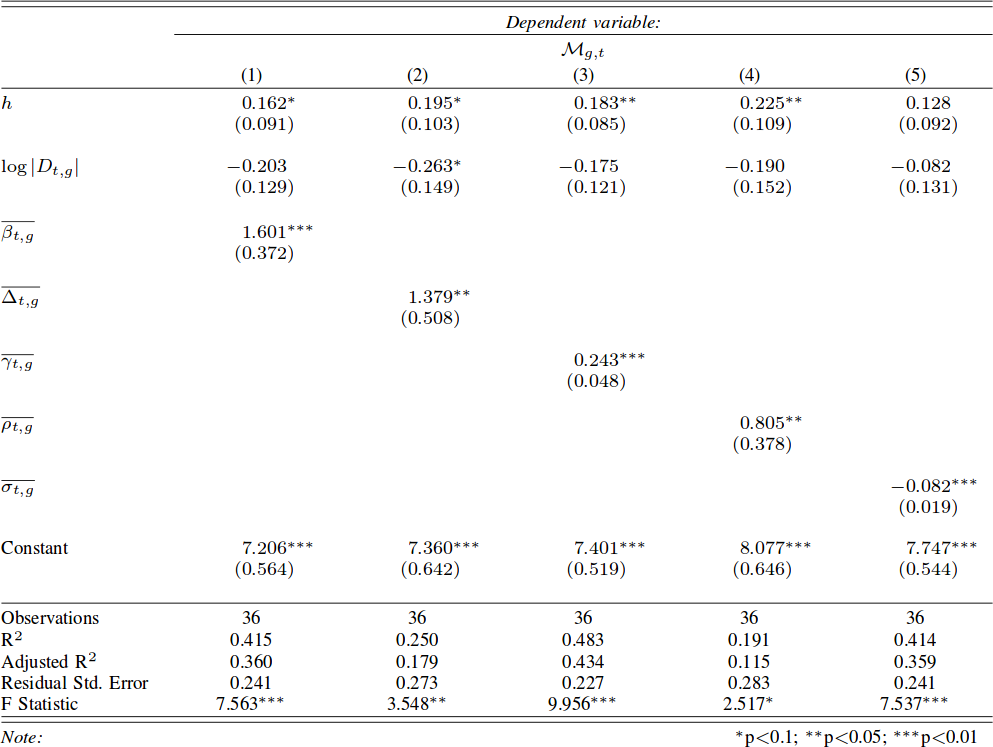
Again: yes. In this case it seems that all calculated features matter to predict meters made. The strongest factor is again leftover connectivity. It means that if the connectivity of the pass network increases after the tackled player is removed from it then the team is able to advance more. Simplifying: if you are able to tackle only low connectivity players, then your opponent is able to gain more territory (p < .01, R2 = 48%).

3. Is it better to build networks of passes and disruptions for each action separately or for the entire match?

The answer to the previous two questions were made by calculating the features on the global match networks. The global network uses all the data from a match, exactly like the pass and disruption edges depicted in the above figure. In principle, one could calculate these features as the match unfolds: sequence by sequence. In fact, networks features at the action level work very well in soccer, as Luca and Paolo already proved. Does that work also in rugby?

Surprisingly, the answer is no. We recalculated the features for each passage of play. A passage of play is the part of a match from when a team gets into possession of the ball until it loses it, scores, or the game flow stops for an infraction. When we calculate features at this level, we find very weak correlations: almost nothing is significant and, when it is, the predictive power is very low. We think that this is because in rugby our definition of sequence is too strict. While soccer is a tactical game — where each sequence counts for itself — rugby is a grand strategy game: sequences build cumulative advantage which pays off after a series of them — or only in the match as a whole.

4. Can we use these relationships to “predict” the outcome of the match?

This is the real queen question of the post, and we do not fully answer it, unfortunately. However, we have a very good reason to think that the answer could be positive. We created a predictor which trains on 17 matches and then, given the global multi-layer network, will pick the winner. You can see the problem of the approach here: we use the network of the match as it happened to “predict” the outcome. However, we did that only because we did not have enough matches for each individual team: we believe we can first predict how pass and disruption networks will shape in a new match using historic data and then use that to predict the outcome. That will be future works, maybe if some team is intrigued by networks and wants to contact us for a collaboration… (wink wink).

The reason I still like to report on our predictor is that it has a very promising property. Its accuracy was 83%. We compared with a prediction made with official rugby rankings, whose performance is worse: 76% accuracy. We also tested against bookmakers, who are better than us with their 86% accuracy. However, historic data on bets only cover more important matches — only 14 out of 18 — and matches between minor teams are usually less predictable. The fact that we are on par on a more difficult task is remarkable. More importantly, bookies tend to just “choose the best team”. For instance, they always predict a New Zealand win. The Haka, however, is not always enough and our networks caught that. New Zealand lost to England in a big upset on December 1st 2012. The bookmakers didn’t see that coming, but our network approach could have.

Continue Reading