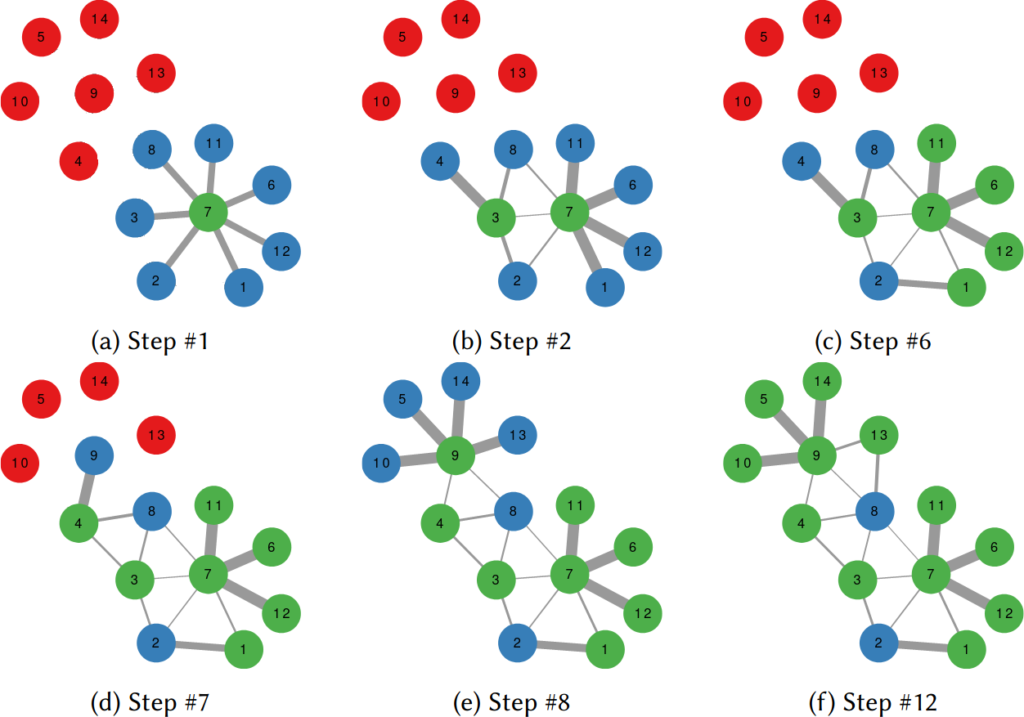
Give Me Some Space!, or: the Slow Descent into Unicode Madness
My wife is the literal embodiment of this comic strip:

She has to overcome the weirdest code golfing issues to get through her research. The other day her issue was: “I have a bunch of text and I want to surround every unicode emoticon with spaces” — the idea being to treat each emoji like a full word.
Sounds easy enough until you get to the word “unicode” and you start hearing helicopters in the background, a Doors song comes on, and you flash memories of going upstream in a jungle river on a barge.
My problem is that, instead, I am the embodiment of the victim in this comic strip:
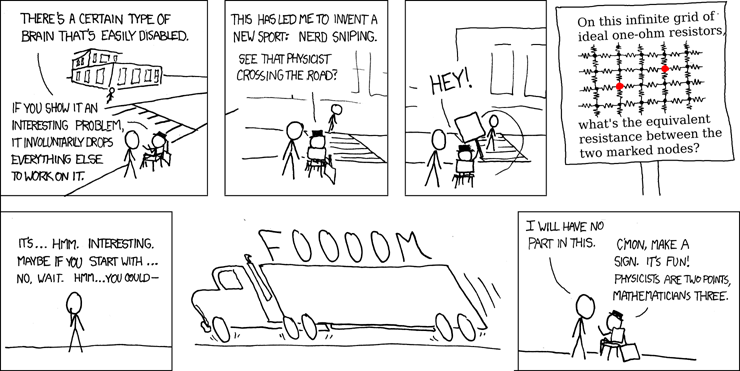
When confronted with something seemingly simple but with an interesting level of complexity behind it, I just have to drop everything I’m doing for my actual job for an hour, until I solve it.
At first glance, it seems easy enough: find a dictionary of emoticons and use it as the basis of a regular expression. The emoji package can take care of the first part. A naive solution could be the following:
import re
from emoji import unicode_codes
allemojis = "".join(unicode_codes.UNICODE_EMOJI['en'])
searcher = re.compile(u'([%s])' % allemojis)
spacemoji = {key: searcher.sub(r' \1 ', texts[key]) for key in texts}
This assumes that “texts” is a dictionary with a collection of texts we’re interested in. The “searcher” wraps a bunch of characters in between square brackets, which means that any matching characters will be found. The the “.sub” method will replace whatever matched (“\1“) with its content surrounded by spaces.
Easy enough. Let’s test it with some example strings:




A passing knowledge of unicode, or a quick Google search about the mysterious \u200d code popping out of nowhere in example #3, leads to a relatively quick diagnosis. Emoticons are not single characters: they can combine multiple unicode characters to modify the appearance of a single glyph. In my case, the baseline turban emoticon is of a male with the baseline yellow emoticon skin tone. To obtain a white lady with a turban you need to combine the turban emoticon with the white color and the woman symbol.
Same goes for numbers: some emoticons contain raw digit characters, and thus those will match even when not “inside” an emoticon.
So here’s a step-by-step cure for our unicode woes:
- Don’t work with string or unicode string objects. Always work with bytestrings by calling “
.encode("utf-8")“. This way you can see what the machine actually sees. It’s not “ “. it’s “
“. it’s “\xf0\x9f\x91\xb3\xf0\x9f\x8f\xbb\xe2\x80\x8d\xe2\x99\x80” (easy, right?). - Don’t use square brackets for your regular expression, because it will only match one character. Emoticons aren’t characters, they are words. Use the pipe, which allows for matching groups of characters.
- Store your emoticons in a list and sort by descending length. The regular expression will stop at the first match, and
 is longer than
is longer than  , because the first one is a modified version. The simple turban emoticon is actually “
, because the first one is a modified version. The simple turban emoticon is actually “\xf0\x9f\x91\xb3” (note how these are the first four bytes of the previous emoticon). So the regular expression will not match the “man with a turban” inside the “white woman with a turban“. - Escape your regular expression’s special characters. Some emoticons contain the raw character “
*“, which will make your compiler scream offensive things at you. - Remember to encode your input text and then to decode your output, so that you obtain back a string and not a byte sequence — assuming you’re one of those basic people who want to be able to read the outputs of their pile of code.
If we put all of this together, here’s the result of my hour of swearing at the screen in Italian 🤌:
import re
from emoji import unicode_codes
allemojis = [x.encode("utf-8") for x in unicode_codes.UNICODE_EMOJI['en']]
allemojis = sorted(allemojis, key = len, reverse = True)
allemojis = b"|".join(allemojis)
searcher = re.compile(b'(%s)' % allemojis.replace(b'*', b'\*'))
spacemoji = {key: searcher.sub(rb' \1 ', texts[key].encode("utf-8")).decode("utf-8") for key in texts}
Which restores some of my sanity:



I’m sure better programmers than me can find better solutions (in less time) and that there are infinite edge cases I’m not considering here, but this was good enough for me. At least I can now go back and do the stuff my employer is actually paying me to do, and I don’t feel I’m in a Francis Ford Coppola masterpiece any more.
 I am an associate prof at IT University of Copenhagen. I mainly work on algorithms for the analysis of complex networks, and on applying the extracted knowledge to a variety of problems.
My background is in Digital Humanities, i.e. the connection between the unstructured knowledge and the coldness of computer science.
I have a PhD in Computer Science, obtained in June 2012 at the University of Pisa. In the past, I visited Barabasi's CCNR at Northeastern University, and worked for 6 years at CID, Harvard University.
I am an associate prof at IT University of Copenhagen. I mainly work on algorithms for the analysis of complex networks, and on applying the extracted knowledge to a variety of problems.
My background is in Digital Humanities, i.e. the connection between the unstructured knowledge and the coldness of computer science.
I have a PhD in Computer Science, obtained in June 2012 at the University of Pisa. In the past, I visited Barabasi's CCNR at Northeastern University, and worked for 6 years at CID, Harvard University.