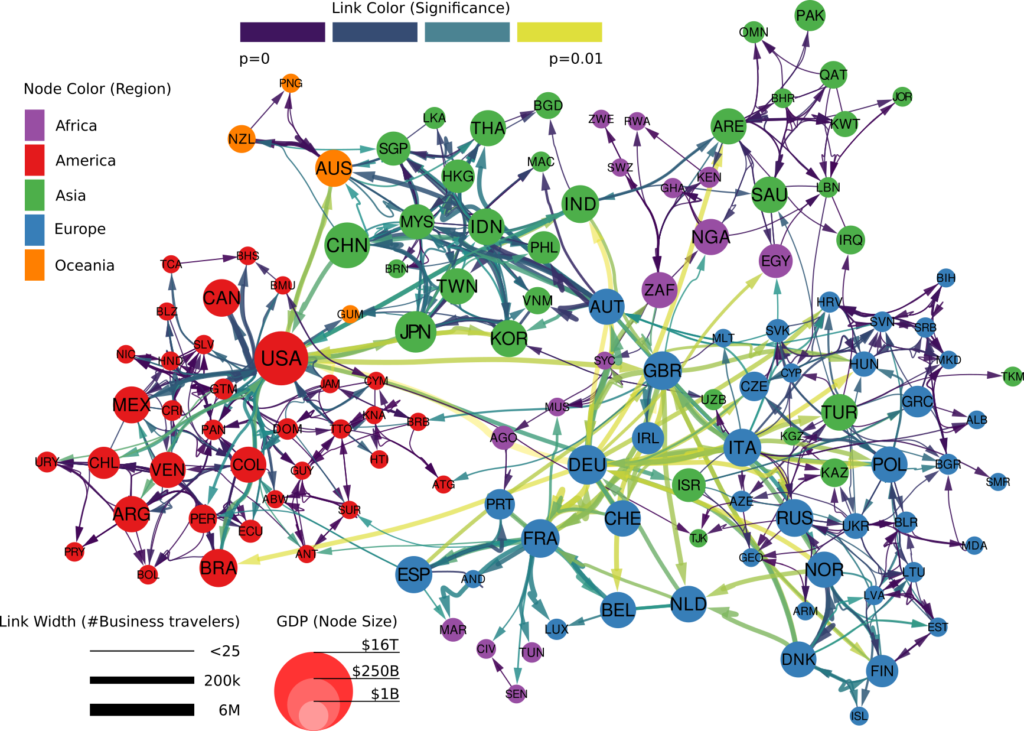
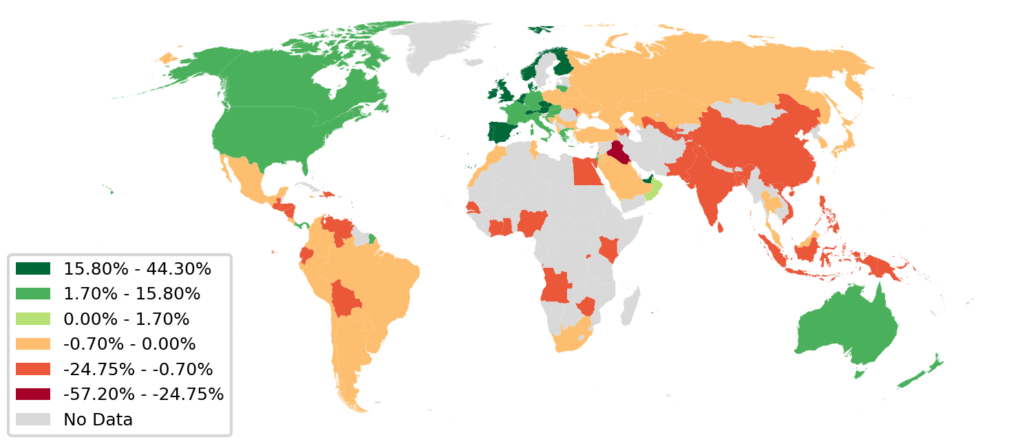
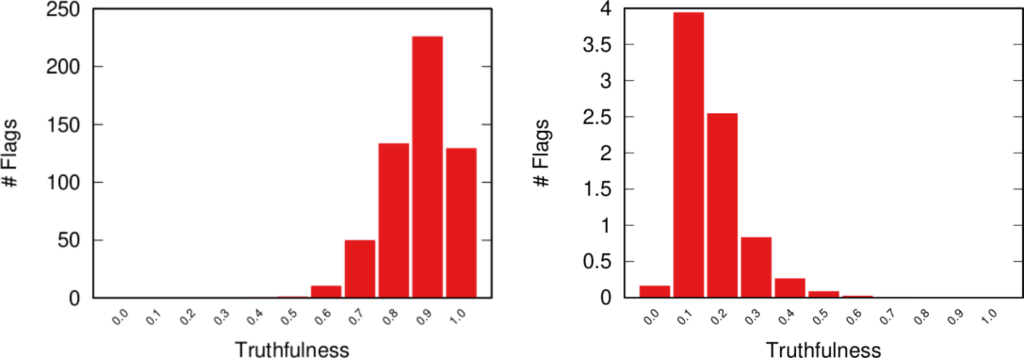
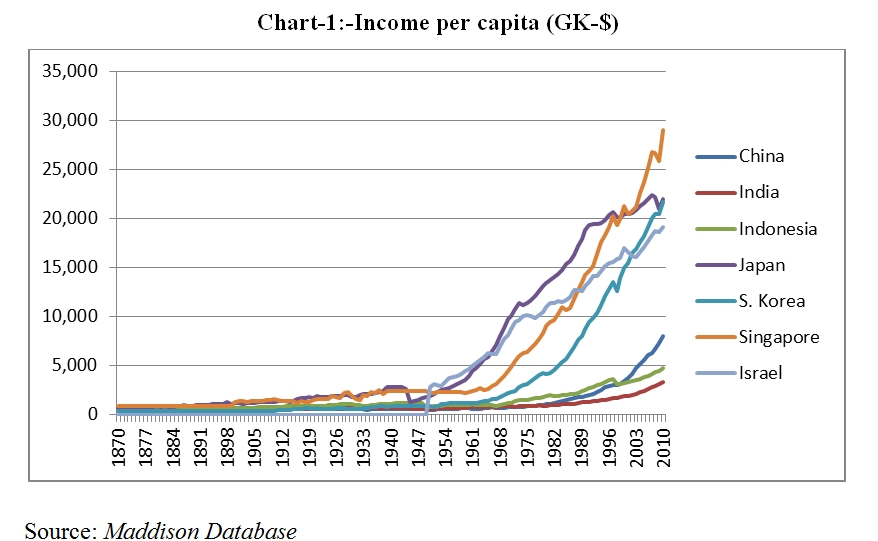
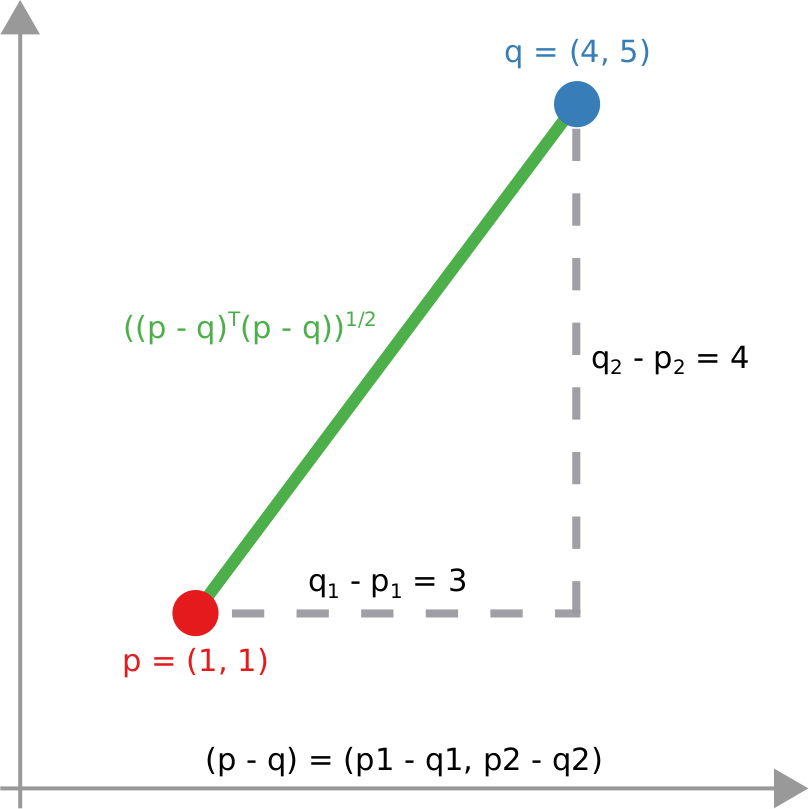
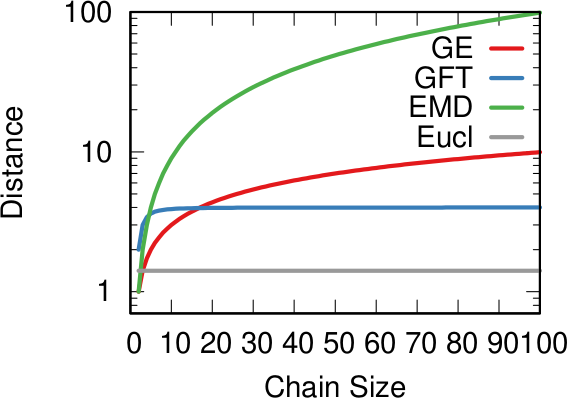
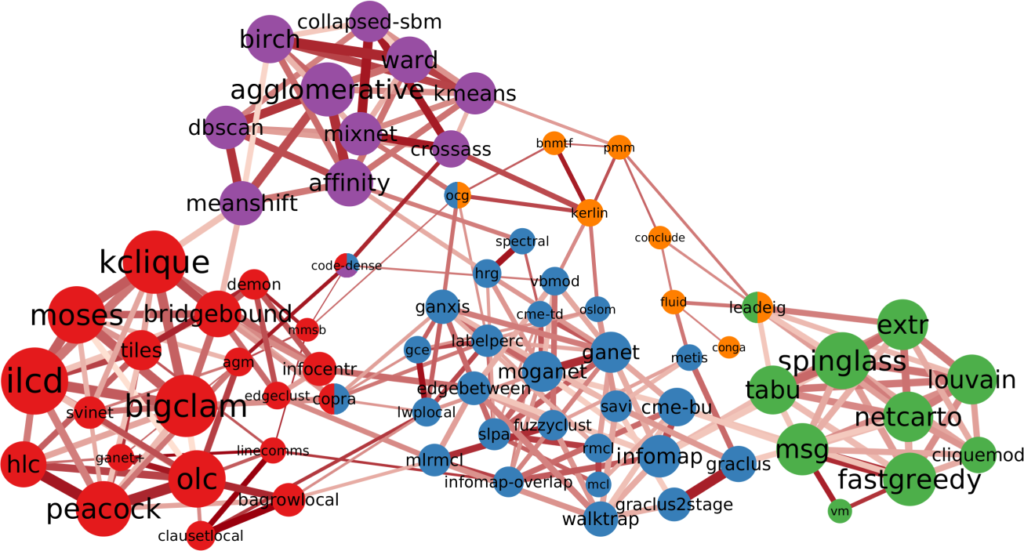
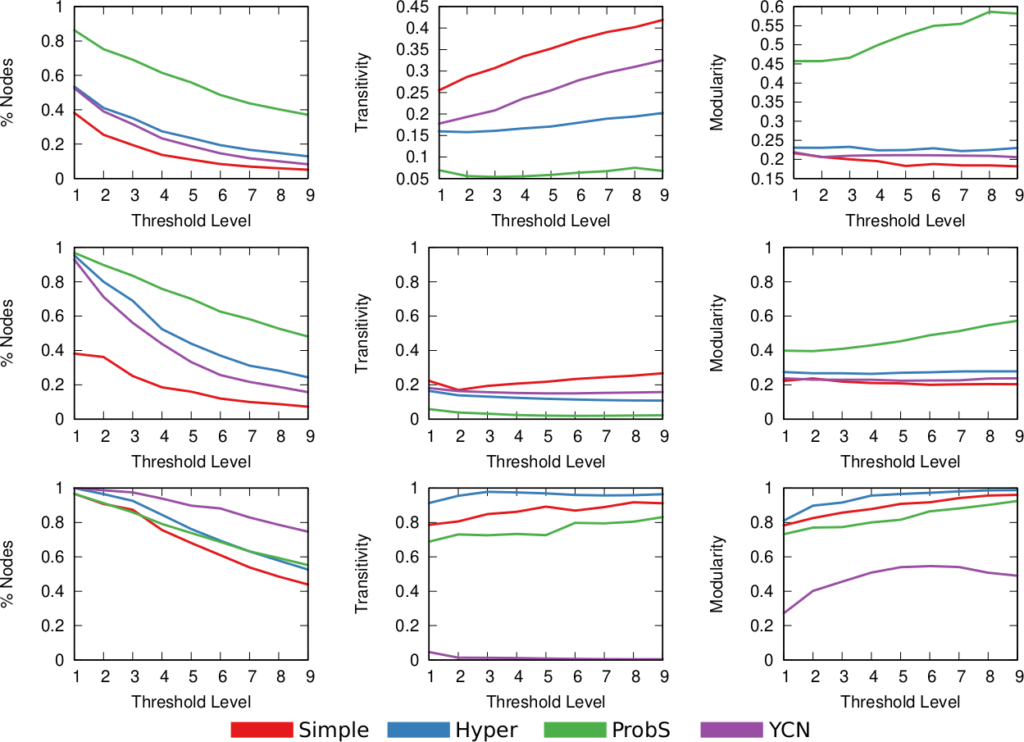
The Atlas for the Aspiring Network Scientist
In the past two years, I’ve been working on a textbook for the Network Analysis class I teach at ITU. I’m glad to say that the book is now of passable enough quality to be considered in version 1.0 and so I’m putting it out for anyone to read for free. It appeared on arXiV yesterday. It is available for download on its official website, which contains the solutions to the exercises in the book. Ladies and gentlemen, I present you The Atlas for the Aspiring Network Scientist.
As you might know, there are dozens of awesome network science books. I cannot link them all here, but they are cited in my atlas’ introduction. So why do we need a new one? To explain why the atlas is special, the best way is to talk about the defects of the book, rather than its strengths.
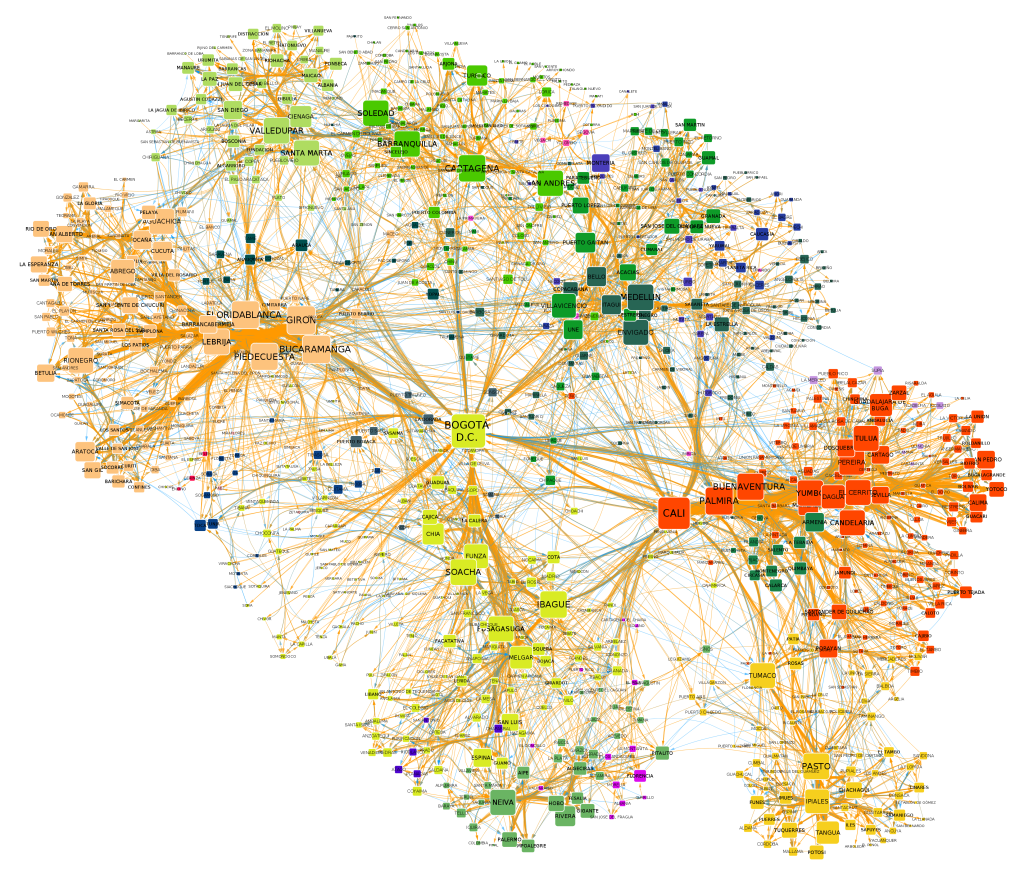
The first distinctive characteristic is that it aims at being broad, not deep. As the title suggests, I wanted this to be an atlas. An atlas is a pointer to the things you need to know, rather than a deep explanation of those things. In the book, I never get tired of pointing out the resources you need to actually understand the nitty-gritty details. When you stumble on a chapter on something you’re familiar with, you’ll probably have the feeling that you know so much more than me — which is true. However, that’s the price to pay if I want to include topics from the Hitting Time Matrix to the Kronecker graph model, from network measurement error to graph embedding techniques. No book I know includes all of these concepts.
The second issue derives from the first: this is a profoundly personal journey of eleven years through network science. No one can, in such a short time, master all the topics I include. Thus there’s an uneven balance: some methods are explained in detail because they’re part of my everyday work. And others are far from my area of expertise. Rather than hiding such a defect, the book wears it on its sleeve. I prefer to include everything I can even if I’m not an expert on it, because the first priority is to let people know that something exists. If I were to wait until I was an expert R programmer before advising you to use iGraph, the book would not exist. If I were to leave out iGraph because I’m not good at it, it would make the book weaker — and give the impression of dishonesty, like the classic Pythonist who ignores R because “it’s the opposing team”.
Finally, the book reads more like a post on this blog than an academic textbook. I use a colorful style and plenty of humor. This is partially as a result of the second point, since the humor is mostly self-deprecating about my limits — for instance, the stabs I take at R are intended as light-hearted jest. In general, I want to avoid being excessively dry and have the readers fall asleep at page 20. This is a risky move, because humor is subjective and heavily culture-dependent. People have been and will be put off by this. If you think I cross the line somewhere in the book, feel free to point that out and ask me to consider your concerns. If, instead, you think that humor in general has no place in academia, then I disagree, but there are plenty alternatives, so you can safely ignore my book.
Given all of the above, it is no surprise that the atlas is imperfect and many things need to be fixed. Trust me that the first draft was significantly worse in all respects. The credit for catching my mistakes goes to my peer reviewers. Every one of their comments was awesome, and every one of the remaining mistakes are only my fault for being unable to address the issues properly. Chief among the reviewers was Aaron Clauset, who read (almost) the entire thing. The others* still donated their time and expertise for free, some of them only asked me to highlight worthwhile charities such as TechWomen and Evidence Action in return.
Given all the errors that remain, consider this a v1.0 of a continuous effort. There are many things to improve: language, concepts, references, figures. Please contact me with any comments. The PDF on the website will reflect changes as soon as is humanely possible. Before I put v1.1 on arXiV, I’ll wait to have a critical mass of changes — I expect to have it maybe for mid to late February.
I also plan to have interactive figures on the website in the future. Version 1.0 was all financed using my research money and time. For the future, I will need some support to do this in my free time. If you feel like encouraging this effort, you can consider becoming a patron on Patreon. A print-on-demand version will be available soon (link will follow), so you could also consider ordering a physical copy — I’ll make 70 juicy cents of profit for every unit sold, because I’m a seasoned capitalist who really knows how to get his money’s worth for two years of labor.
I poured my heart in this. I really hope you’ll enjoy it.
* Special thanks go to Andres Gomez-Lievano. The other peer reviewers are, in alphabetical order: Alexey Medvedev, Andrea Tagarelli, Charlie Brummitt, Ciro Cattuto, Clara Vandeweerdt, Fred Morstatter, Giulio Rossetti, Gourab Ghoshal, Isabel Meirelles, Laura Alessandretti, Luca Rossi, Mariano Beguerisse, Marta Sales-Pardo, Matte Hartog, Petter Holme, Renaud Lambiotte, Roberta Sinatra, Yong-Yeol Ahn, and Yu-Ru Lin.
 I am an associate prof at IT University of Copenhagen. I mainly work on algorithms for the analysis of complex networks, and on applying the extracted knowledge to a variety of problems.
My background is in Digital Humanities, i.e. the connection between the unstructured knowledge and the coldness of computer science.
I have a PhD in Computer Science, obtained in June 2012 at the University of Pisa. In the past, I visited Barabasi's CCNR at Northeastern University, and worked for 6 years at CID, Harvard University.
I am an associate prof at IT University of Copenhagen. I mainly work on algorithms for the analysis of complex networks, and on applying the extracted knowledge to a variety of problems.
My background is in Digital Humanities, i.e. the connection between the unstructured knowledge and the coldness of computer science.
I have a PhD in Computer Science, obtained in June 2012 at the University of Pisa. In the past, I visited Barabasi's CCNR at Northeastern University, and worked for 6 years at CID, Harvard University.